Research

Mathematical aspects of identifying entangled quantum states (entanglement witnesses, nonlinear entanglement criteria, spin squeezing inequalities)

• Methods for the experimental creation and detection of entanglement in quantum optical systems (photonic systems, spin squeezing in cold atomic ensembles, optical lattices of cold atoms)
• Entanglement detetcion in Dicke states realzied with photons (collaboration with the group of Harald Weinfurter, MPQ, Munchen)
• Multi-particle singlet states in cold gases (collaboration with the group of Morgan W. Mitchell at ICFO)
• Entanglement detetcion in Dicke states realized with cold gases (collaboration with the group of Carsten Klempt, Hannover)
• Scalable state tomography (Permutationally Invariant Quantum Tomography, collaboration with the group of Harald Weinfurter, MPQ, Munchen)
• Application of entangled quantum states for quantum metrology (e.g., differential magnetometry with cold atomic ensembles)
• Quantum metrology, quantum Fisher Information and its relation to multipartite entanglement
• Foundations of quantum theory (Bell inequalities and local hidden variable models)

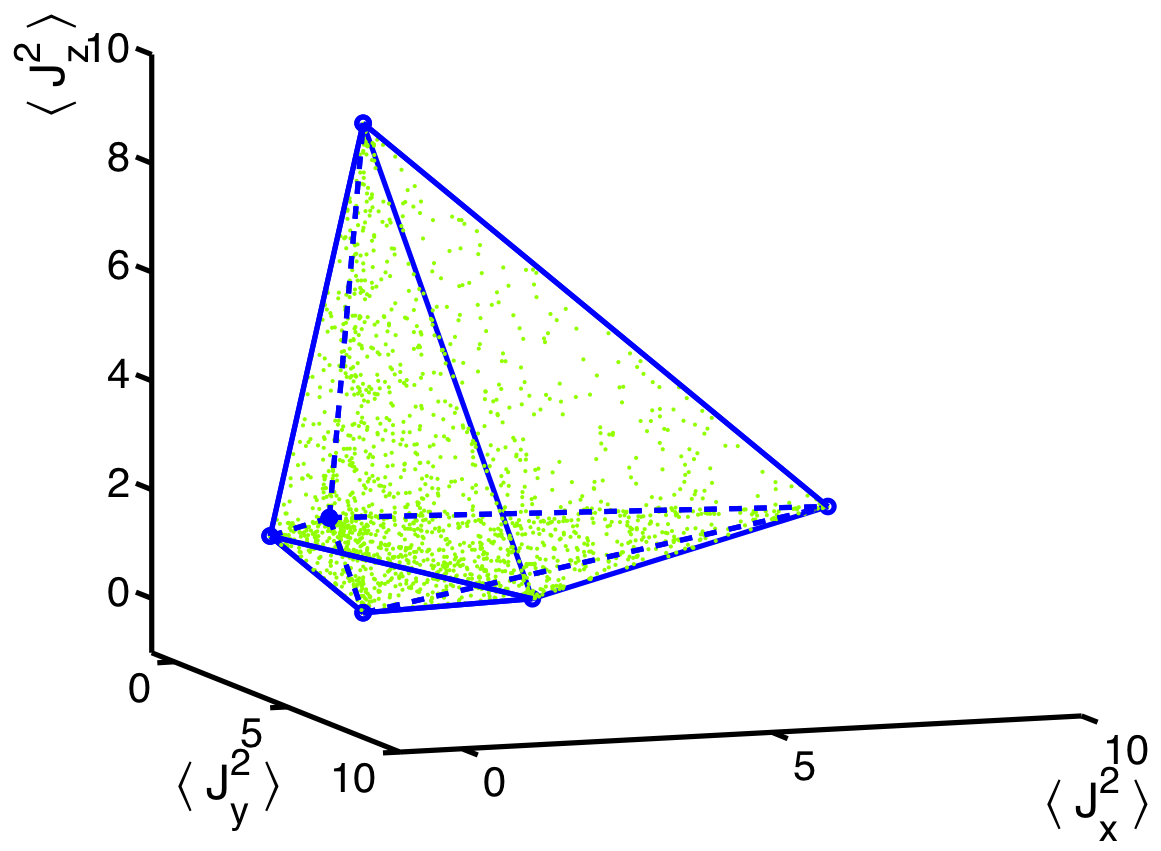
1. Polytope of separable states for the Optimal Spin Squeezing Inequalities. [Figure from Phys. Rev. Lett. 99, 25045 (2007); Phys. Rev. A 79, 042334 (2009).]

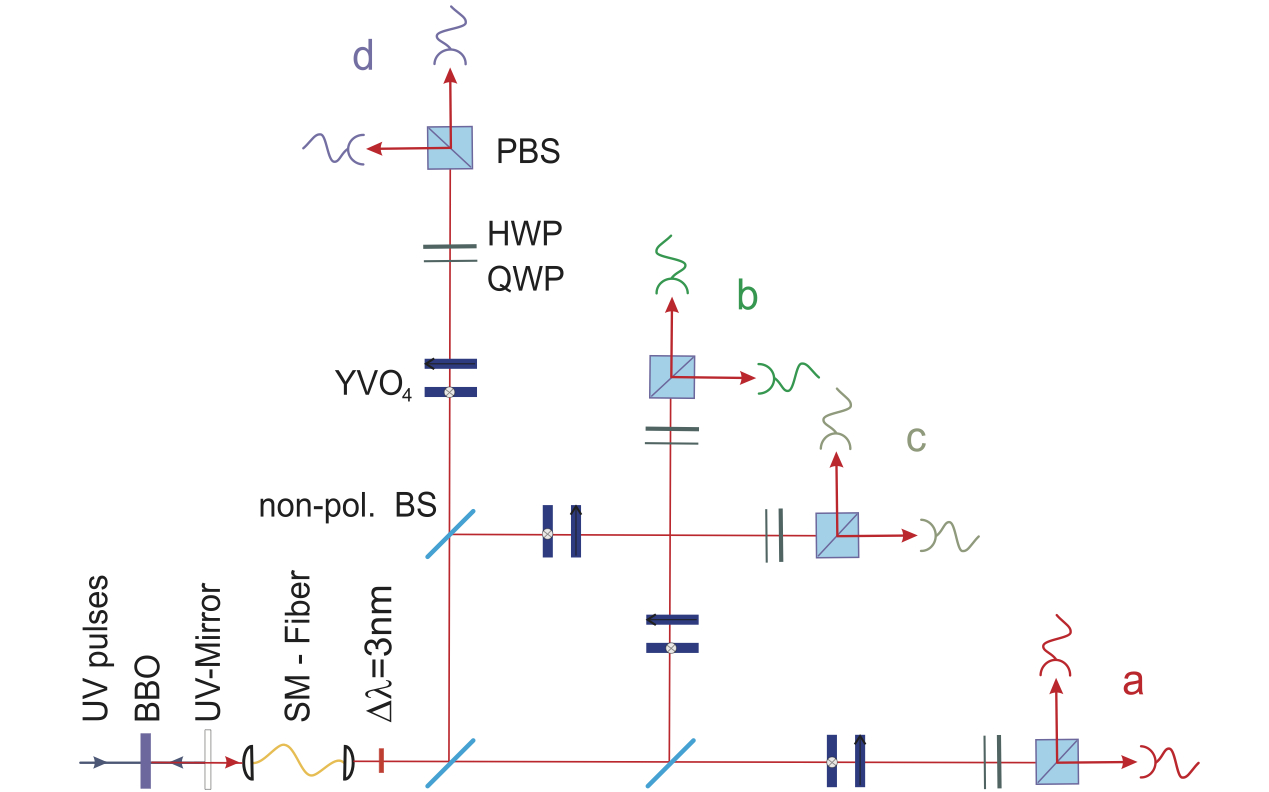
2. Setup generating a four-qubit symmetric Dicke state with two excitations with parametric down-conversion in a BBO crystal, linear optical elements and detectors. [Figure from Phys. Rev. Lett. 98, 063604 (2007).]

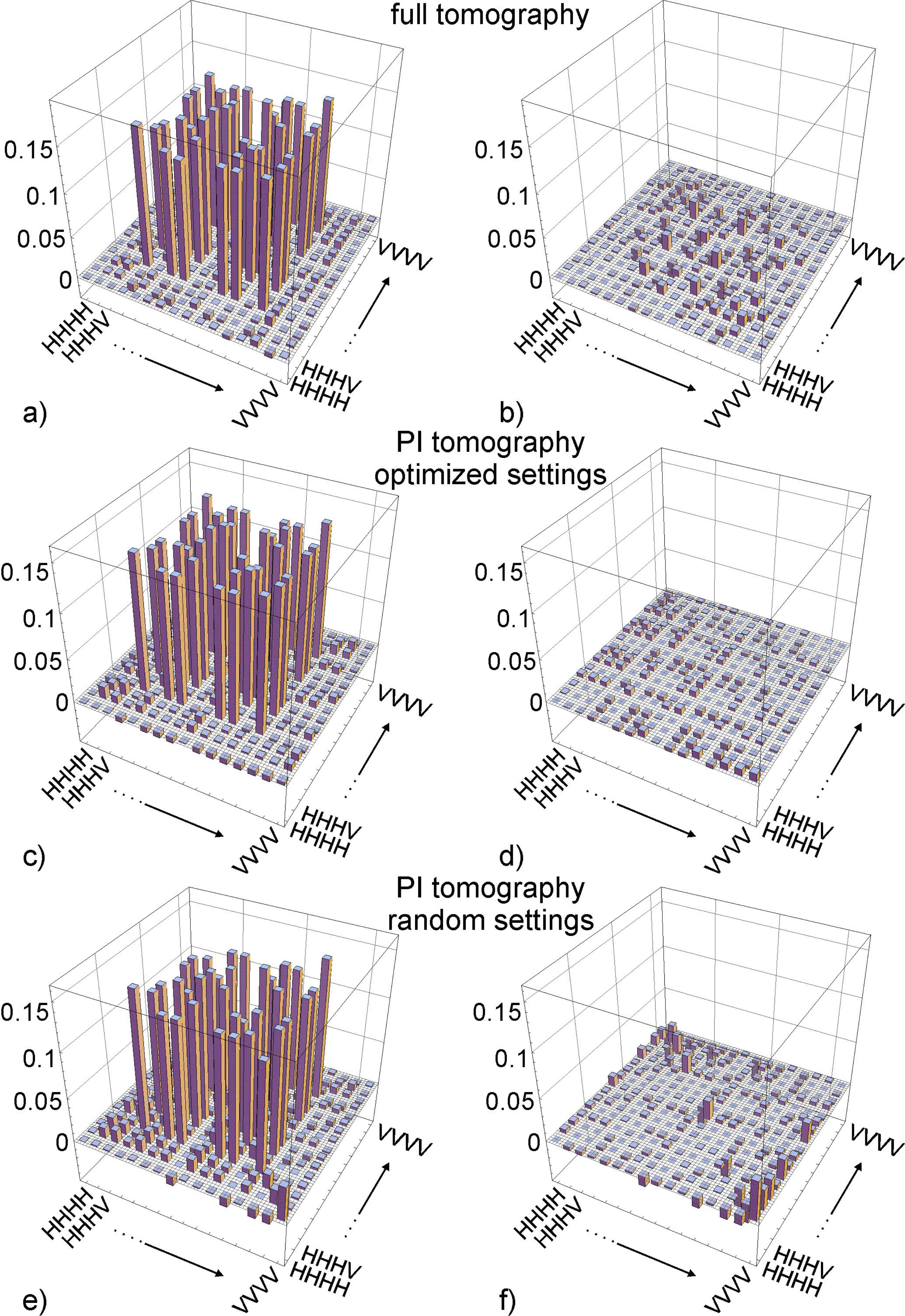
3. Results of Permutationally Invariant Tomography in a four-photon experiment [Figure from Phys. Rev. Lett. 105, 250403 (2010).]

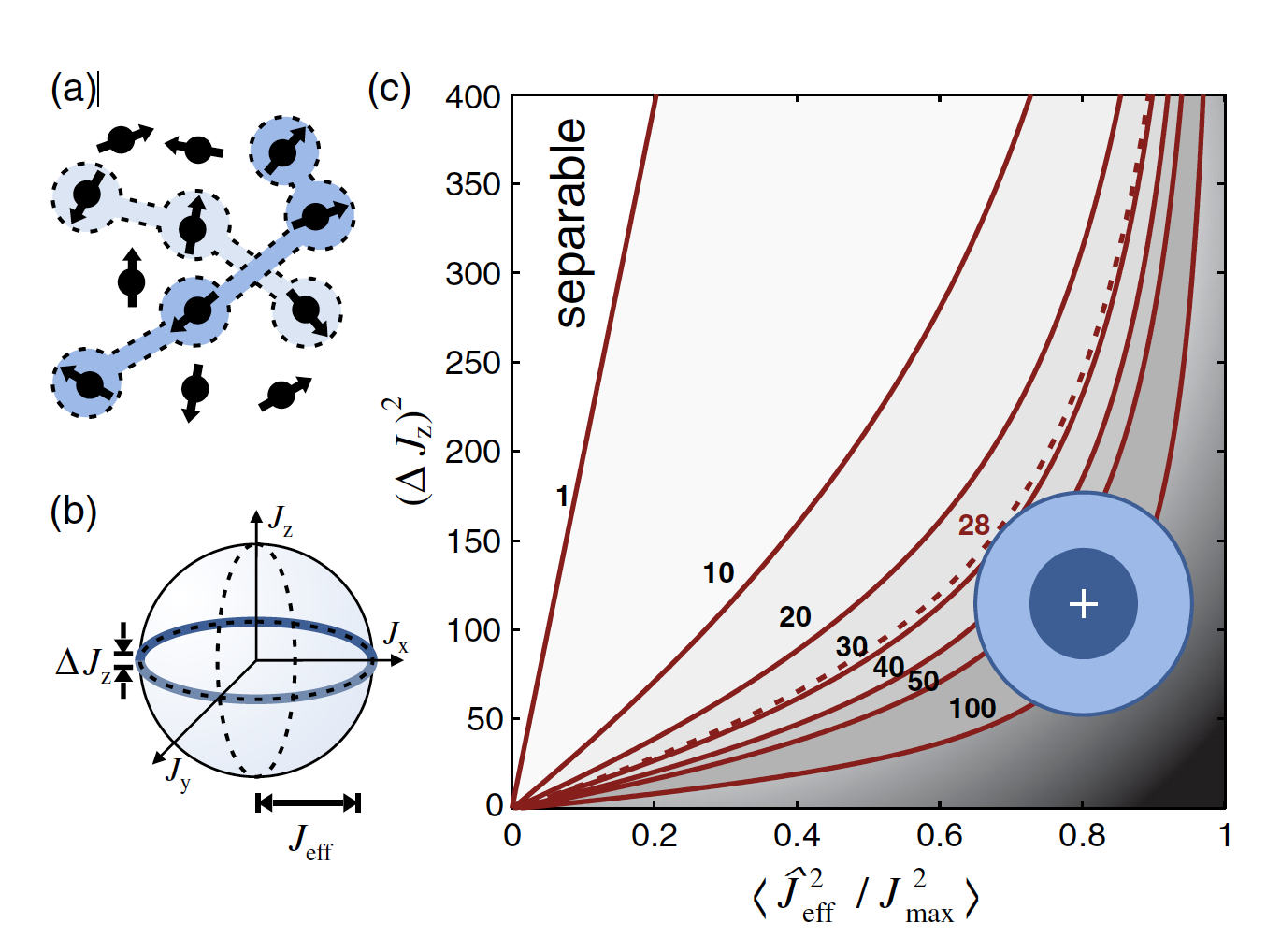
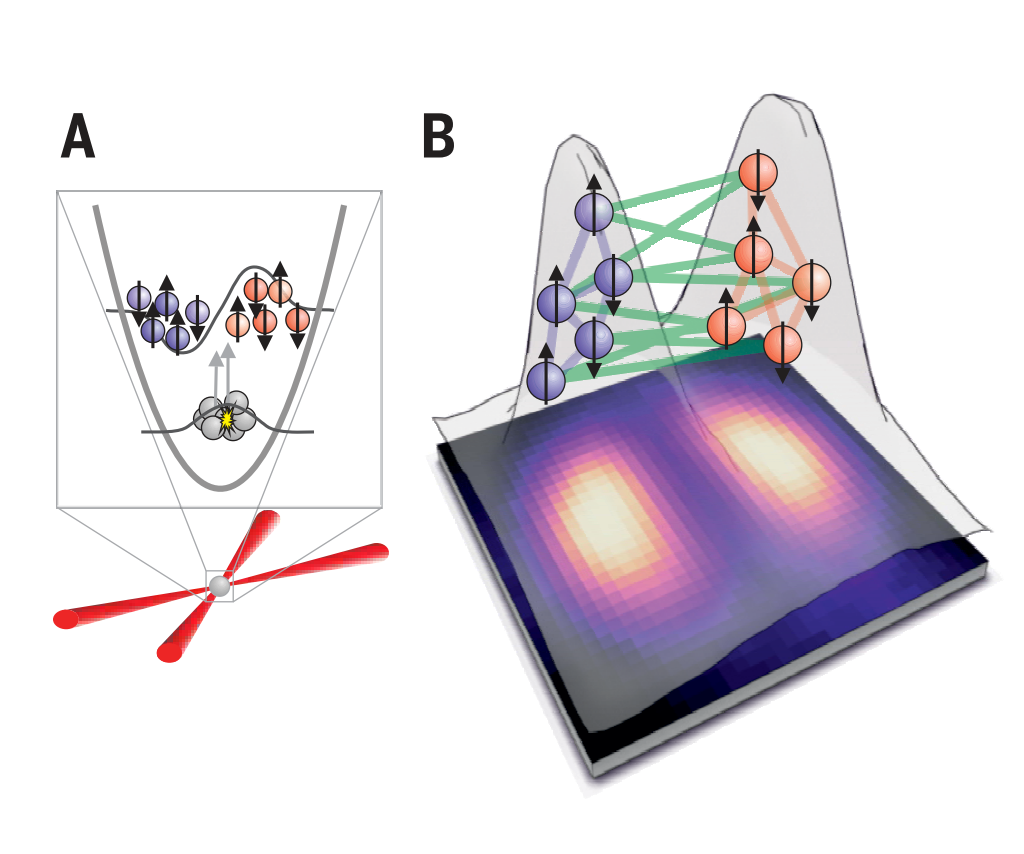
4. Multipartite entanglement in Dicke states created with cold gases [Figure from Phys. Rev. Lett. 112, 155304 (2014). ]

5. Bipartite entanglement in Dicke states created with cold gases [Figure from Science 360, 416 (2018).]